Polinomios de Taylor
Contenido
¿ Qué son los Polinomios de Taylor ?
Cuando estudiamos la vídeo clase de las Series de Taylor y de Mclaurin pudimos observar como las funciones que son diferenciables infinitamente generan unas series de potencias conocidas como Series de Taylor. Estas series tienen la utilidad de que nos ofrecen unas aproximaciones en forma de polinomios de las funciones que las han generado en torno al punto x=a.
Para recordar un poco, decíamos que la serie de Taylor generada por f(x) en torno a x=a es:
En el caso de la serie de McLaurin tendríamos que a=0, es decir, no es mas que la serie de Taylor particularizada para el punto x=0.
Definición de Polinomios de Taylor
Sea f(x) una función con derivadas de orden k para k=1,2,…,N en torno a un punto x=a. Se define el polinomio de Taylor de orden n generado por la función f(x) en un entorno de x=a como:
Siempre vamos a hablar de polinomio de Taylor de orden n y no de grado n. Este es un error muy común que conviene evitar. La explicación es sencilla; si suponemos que tenemos f(x)=cos(x), los dos primeros polinomios de Taylor en x=0 serán: y
. Podemos observar que el polinomio de primer orden tiene grado cero y no uno.
Es interesante notar que el polinomio de Taylor de orden 1 de nuestra función f(x) en un punto x=a es una linealización de dicha función en el entorno de ese punto. De la fórmula nos quedaríamos con los dos primeros sumandos.
Se aprecia claramente que tenemos la ecuación de una recta, por eso lo de linealización.
¿Para qué se usan los polinomios de Taylor?
En el inicio de esta explicación avanzábamos que la utilidad de estos polinomios de Taylor no era otra que ofrecer aproximaciones polinomiales en el entorno del punto en el cual expandíamos la función.
En la primera vídeo clase resolvemos el caso de calcular los polinomios de Taylor para la función , vamos a expresar las soluciones con el fin de explicar y detallar la utilidad de estos polinomios de Taylor . El polinomio de Taylor de orden n de dicha función entorno a x=0 lo calculamos en la vídeo clase y es :
Vamos a centrarnos en los polinomios de los órdenes 1, 2 y 3. Tendríamos:
, este sería el polinomio de orden 1
, este sería el polinomio de orden 2
, este sería el polinomio de orden 3
Una vez que tenemos los polinomios de Taylor de órdenes 1,2 y 3 vamos a representarlos gráficamente junto con la función original en torno al punto x=0 para poder entender mejor, con la ayuda de la gráfica el sentido de estos polinomios.
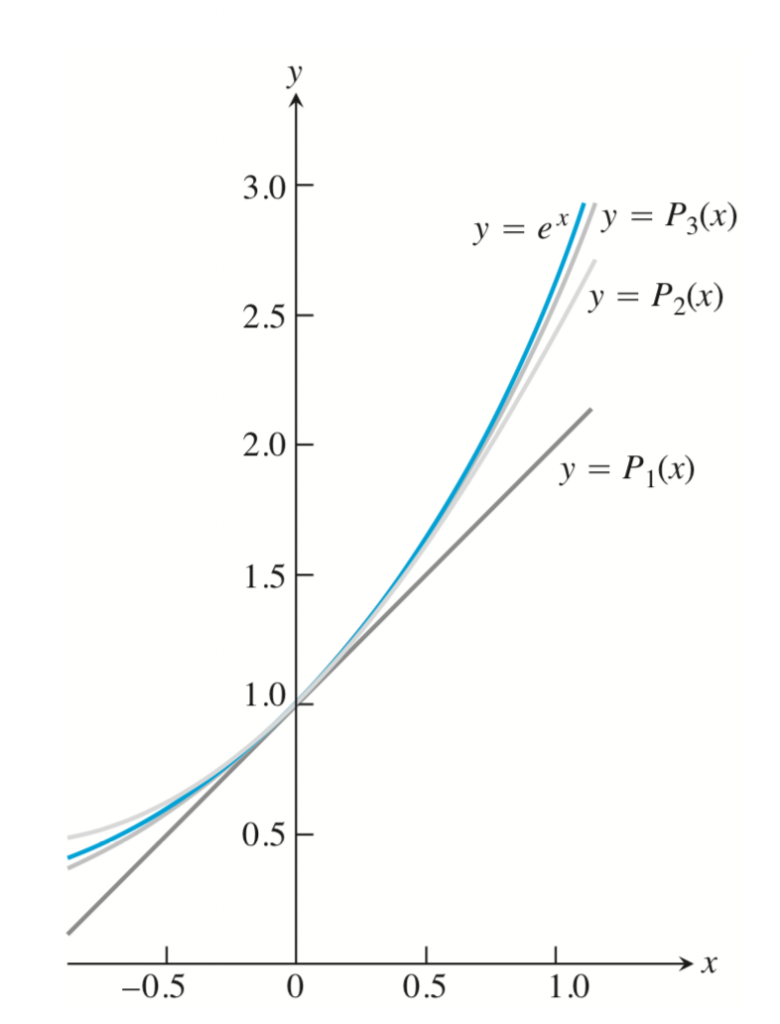
Podemos observar como a medida que aumenta el orden del polinomio de Taylor de nuestra función dicho polinomio se aproxima mucho más a la función, en torno al punto de estudio, siendo además no sólo más precisa la aproximación sino también más amplio el rango de valores de x entorno al punto x=0, en este caso, donde el polinomio de Taylor presenta una convergencia aceptable con la función.
Llegados a este punto te preguntarás que para qué necesito un polinomio de Taylor que se aproxime a una función en torno a un punto si ya tengo la función. La respuesta es sencilla; es mucho más fácil trabajar con un polinomio de Taylor que con su función, ya que derivar, integrar u operar con un polinomio es rápido y sencillo mientras que con la función puede resultar muy engorroso. En el caso que he puesto como ejemplo puede parecer que la función es tan fácil de usar como sus polinomios de diferentes órdenes pero imagina que tuviésemos una función mucho más compleja con alguna función trigonométrica multiplicada por una potencia.
A continuación, te dejo las vídeo clases, a medida que vaya subiendo más al canal de YouTube éstas irán apareciendo aquí. Espero que te resulte útil y no olvides suscribirte al canal.
Cálculo de los Polinomios de Taylor
![]()
![]()

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.
 Suscríbete a mi canal
Suscríbete a mi canal