Derivadas | La guía definitiva!

50 comentarios / Derivadas, Matemáticas / Por

¿Quién inventó las derivadas?

Las derivadas, en el contexto de cálculo matemático, no fueron inventadas por una sola persona, sino que se desarrollaron a lo largo de varios siglos con contribuciones de varios matemáticos importantes. Sin embargo, Isaac Newton y Gottfried Wilhelm Leibniz son ampliamente reconocidos como los co-inventores del cálculo, que incluye el concepto de derivada.

Isaac Newton, un matemático y físico inglés, desarrolló el cálculo en la segunda mitad del siglo XVII. Newton utilizó el concepto de “fluxiones” para describir el cambio instantáneo en una cantidad variable, que es esencialmente lo que ahora llamamos derivada.

Gottfried Wilhelm Leibniz, un filósofo, matemático y científico alemán, también desarrolló el cálculo en la misma época. Leibniz introdujo la notación de diferenciación que todavía utilizamos hoy en día, incluyendo el uso de la notación “d/dx” para denotar la derivada de una función.

Ambos matemáticos hicieron contribuciones significativas al desarrollo del cálculo, y aunque hubo una controversia histórica sobre quién lo inventó primero, hoy en día se les atribuye a ambos de manera conjunta. La invención del cálculo revolucionó las matemáticas y tuvo un impacto profundo en la física y otras ciencias, permitiendo el estudio de fenómenos de cambio y movimiento de una manera más precisa y poderosa.

derivadas
Gottfried Wilhelm Leibniz.*oil on canvas.*81 x 66 cm.

Significado de las derivadas

Formalmente, cuando calculamos la derivada de una función lo que estamos calculando es el valor de un límite que mide la razón a la que cambia dicha función con respecto a su variable, respecto a la que derivamos.  Las derivadas se usan para el cálculo de velocidades, aceleraciones, optimizar funciones, y una infinidad más de utilidades. Nos vamos a centrar en este texto simplemente en el cálculo de la derivada de una función y las reglas de derivación existentes para ello, quedándonos por ahora con la idea que hemos mencionado al principio. En temas posteriores las desarrollaremos.

 

Definición de derivadas

La derivada de la función f(x) con respecto a la variable x, en el punto x=a es:

f'\left( a\right) =\lim _{h\rightarrow 0}\dfrac {f\left( a+h\right) -f\left( a\right) }{h}

si este límite existe.

Una definición equivalente de la derivada es también la siguiente:

f'\left( a\right) =\lim _{x\rightarrow a}\dfrac {f\left( x\right) -f\left( a\right) }{x-a}

¿Cómo se escriben las derivadas de las funciones?

La forma de escribir correctamente la derivada de una función es la siguiente:

\dfrac {d}{dx}f\left( x\right) =\dfrac {d}{dx}y\left( x\right) =Df_{x}\left( x\right)

en esta expresión queda perfectamente patente que estamos derivando la función f(x) respecto a la variable x. Cualquiera de las tres expresiones de la derivada con respecto a x es totalmente correcta. La función a derivar suele llamarse normalmente f(x) ó y(x). Sin embargo, es muy frecuente encontrar la siguiente notación o forma de escribir las derivadas:

y'\left( x\right) =f'\left( x\right)

Ambas expresiones de la derivada son correctas y si bien la fórmula anterior es la más utilizada por su sencillez, no queda reflejada respecto a qué variable se deriva, aunque está implícito. Para terminar, diremos que ambas notaciones son correctas y que se usan indistintamente en la bibliografía existente, pudiendo afirmar que:

f'\left( x\right) =\dfrac {d}{dx}f\left( x\right) =\dfrac {df\left( x\right) }{dx}

lo que es equivalente a la siguiente expresión dependiendo de cómo se llame la función f(x) ó y(x):

y'\left( x\right) =\dfrac {d}{dx}y\left( x\right) =\dfrac {dy\left( x\right) }{dx}

 

Cálculo de las derivadas a partir de la definición

El proceso de cálculo de la derivada de una función se llama diferenciación. Siempre se deriva o diferencia, se usa mayoritariamente la primera palabra, respecto a una variable, normalmente  x, de forma genérica y una vez que hemos obtenido la derivada sustituimos en la x el punto donde queremos calcular la derivada, particularizando así el valor de ésta. La forma de calcular la derivada usando la definición consiste en aplicar la fórmula de la definición. En el siguiente vídeo os explico un ejercicio práctico en el que calculamos el valor en un punto de la derivada de una función usando su definición mediante el límite.

Cálculo de las derivadas de las funciones

Nunca se usa la definición de la derivada de una función para calcular su función derivada ya que es un proceso largo y demasiado complejo, máxime cuando existe otro método mucho más rápido y sobre todo menos propenso a cometer errores. Sin embargo, en algunos exámenes suele preguntarse al alumno que calcule la derivada de una función mediante la aplicación de la definición para que el alumno demuestre que tiene destreza calculando el límite de la función que es necesario.

Para calcular la derivada de una función vamos a usar la Tabla de derivadas o Tabla de fórmulas de derivadas junto con las reglas de derivación. Estas fórmulas no aparecen por arte de magia, sino que se infieren mediante un proceso de inducción que consiste en derivar aplicando la definición de derivada a funciones genéricas para así obtener una regla que permita derivarla.

Reglas de derivación

Sean f(x)  y g(x)  dos funciones que vamos a denotar por f  y g .

Derivada de la suma/resta de dos funciones

 \left( f\pm g\right) '=f'\pm g' La derivada de una suma/resta de dos funciones es la suma/resta de las derivadas de estas funciones.

Derivada del producto de dos funciones

 \left( f\times g\right) '=f'\times g+f\times g' La derivada del producto de dos funciones es igual a la derivada de la primera función por la segunda sin derivar más la primera sin derivar por la segunda derivada.

Derivada del cociente de dos funciones

 \left( \dfrac {f}{g}\right) ^{'}=\dfrac {f'\cdot g-f\cdot g'}{\left( g\right) ^{2}} La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador sin derivar menos el numerador sin derivar por la derivada del denominador, todo ello dividido entre el denominador al cuadrado.

Derivada del producto de una constante a por una función

 \left( a\cdot f\right) '=a\cdot f' La derivada de una función por una constante es la deriva de la función por la constante sin derivar.

Regla de la cadena

Permite derivar una función que es composición de varias funciones. Matemáticamente se expresa por:

\left[ g\left( f\left( x\right) \right) \right] '=g'\left( f\left( x\right) \right) \cdot f'\left( x\right)

Esto se entenderá perfectamente cuando resolvamos ejercicios.

Tabla de derivadas. Fórmulas de derivadas o formulario de derivadas

La tabla de derivadas contiene las fórmulas de las derivadas para todos los tipos de funciones más frecuentes. Para poder usarla sólo hay que identificar la función que queremos derivar y aplicar la correspondiente fórmula. Descarga la siguiente tabla con las reglas de derivación y fórmulas de derivadas, la hice yo mismo y te puedo asegurar que es la mejor que vas a encontrar en la web. Descárgala, es gratis, pinchando en la siguiente imagen.

tabla de derivadas

 

Derivada de una constante

 f\left( x\right) =k f'\left( x\right) =0

Derivada de una función elevada a una constante

y=\left[ f\left( x\right) \right] ^{n}

 y'=n\cdot f'\left( x\right) \cdot \left[ f\left( x\right) \right] ^{n-1}

Derivada función exponencial neperiana

 y=e^{f\left( x\right) } y'=f'\left( x\right) e^{f\left( x\right) }

Derivada función exponencial

y=a^{\left( f\left( x\right) \right) } y'=f'\left( x\right) a^{\left( f\left( x\right) \right) }\ln a

Derivada función logarítmica

 y=\ln f\left( x\right) y'=\dfrac {f'\left( x\right) }{f\left( x\right) }

Derivada función seno

 y=\sin \left( f\left( x\right) \right) y'=f'\left( x\right) \cos \left( f\left( x\right) \right)

Derivada función coseno

 y=\cos \left( f\left( x\right) \right) y'=-f'\left( x\right) \sin \left( f\left( x\right) \right)

Derivada función tangente

 y=\tan \left( f\left( x\right) \right) y'=\dfrac {f\left( x\right) }{\cos ^{2}f\left( x\right) }

Derivada función potencial exponencial

 y=\left( f\left( x\right) \right) ^{g\left( x\right) } y'=y\left[ g'\ln \left( f\right) +g\dfrac {f'}{f}\right]

 

Ejercicios resueltos paso a paso de derivadas. Regla de la cadena.

Aprender a derivar funciones es sinónimo de hacer muchos ejercicios de derivadas, cuantos más ejercicios de derivadas resuelvas más rápido vas a aprender a derivar. En los siguientes vídeos de derivadas explico paso a paso cómo aplicar las reglas de derivación, las fórmulas que nos permiten encontrar la derivada de una función, y después hago muchos ejercicios aplicando esa fórmula. Suscríbete al este canal de YouTube para estar al corriente de los nuevos vídeos que se van publicando.

subscribeSuscríbete a mi canal
«
Anterior
1
/
1
Siguiente
»
loading
play
Cómo calcular Derivadas | Aprende desde cero #1
play
Cómo calcular Derivadas | Aprende desde cero #2
play
Cómo calcular Derivadas | Aprende desde cero #3
play
Cómo calcular Derivadas | Aprende desde cero #4
play
Cómo calcular Derivadas | Aprende desde cero #5
play
Cálculo de la derivada de una funcion | Curso básico | Parte 6
«
Anterior
1
/
1
Siguiente
»
loading

 

Ejercicios resueltos de exámenes de derivadas. Regla de la cadena.

Ejercicios de derivadas resueltos paso a paso usando las fórmulas de la tabla de derivadas. Los ejercicios de derivadas se resuelven de forma fácil y sencilla para el alumno a fin de que pueda seguir la vídeoclase sin quedarse atrás.

subscribeSuscríbete a mi canal
«
Anterior
1
/
1
Siguiente
»
loading
play
Cálculo de derivadas | Ejercicios resueltos paso a paso | Parte 1
play
Cálculo de derivadas | Ejercicios resueltos paso a paso | Parte 2
play
Cálculo de derivadas | Ejercicios resueltos paso a paso | Parte 3
play
Cálculo de derivadas | Ejercicios resueltos paso a paso | Parte 4
play
Cálculo de derivadas | Ejercicios resueltos paso a paso | Parte 5
play
Cálculo de derivadas | Ejercicios resueltos paso a paso | Parte 6
«
Anterior
1
/
1
Siguiente
»
loading



Vistas: 401.044

Entradas relacionadas

50 comentarios en “Derivadas | La guía definitiva!”

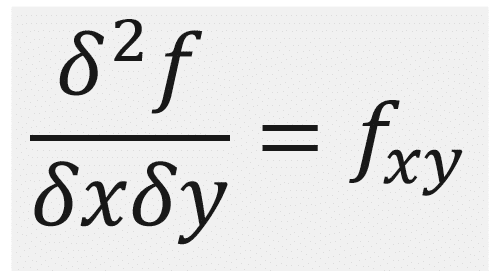
  1. Pingback: Derivadas – El estrés de 2º de BACH

  2. Ander

    En la tabla de las derivadas, la derivada de la tangente de una función es la derivada de esa función entre el coseno al cuadrado de esa función. Llevo un tiempo ya viendo tus vídeos y me encantan y he aprendido muchas cosas, gracias x todo. <3

    Responder
  6. Romina Gomez

    Hola, soy de Argentina y estoy compilando material para repaso a mis alumnos de microeconomía, me interesa tus constenidos para su consulta, voy a recomendarles que lo visiten! Saludos

    Responder
  8. Ariz

    Me encantó el material, y nunca le había entendido, otras personas intentaban explicarme como si supiera, pero lo manejas desde cero y ahora comprendo las conceptualizaciones, con solo leer a detalle esta super explicado.. Gracias y saludos!!!

    Responder
  14. Johana Cabrera

    Me gusto mucho la explicación, es muy claro en el tema.
    Pregunta: Cuenta con ejercicios que acompañado al material para practicar?

    Responder
  15. Graciela Aleman

    Graciasss muy buena la explicación! Empese a estudiar para Prof de Fisica y tus vídeos me sirvieron bastante mil de Gracias.

    Responder
  17. Vir

    Hola
    Acabo de empezar la carrera de ADE y después de tantos años sin tocar las mates voy un poco perdida con las derivadas y por lo tanto con la asignatura de Microeconomia. Estos videos me sirven para esta asignatura?
    Gracias

    Responder
  18. Vir

    Hola Fran, he empezado la carrera de ADE por la UNED este año y la verdad que hace años que yo termine mis estudios y ando perdida con el tema de las derivadas para la asignatura de Microeconomia.
    Tus videos me pueden ayudar para esta asignatura??
    Me acabo de suscribir a tu canal
    Gracias

    Responder
  20. Alfredo Gutierrez

    Gracias por tu aporte…acabo de descubrir tu canal, me gusta como explicas, en particular mi profe de mate no me gusta como explica…

    Responder
  28. CRISTINA MARTINEZ

    Hola te felicito por compartir tus conocimientos.
    te seré franca se me dificulta todo se que es por que no tengo las bases. Entre a una carrera en línea en la cual llevo calculo integral y no he podido resolver nada, comenzamos con figuras amorfas y aun sigo ahí,
    que me recomiendas

    Responder
  30. Cristian

    Genial y maravilloso.
    Estoy ejerciendo de CEO de una gran empresa y me he matriculado en ADE, pero hace ya 10 años que terminé el bachiller de ciencias, con lo que hasta las matematicas de microeconomia me estan pareciendo dificiles.
    Videos geniales, faciles y claros. Perfecto.
    Muy buen trabajo.

    Responder

Deja un comentario