Conceptos a tratar: números complejos, unidad imaginaria, potencias de la unidad imaginaria, suma y resta de números complejos, producto de un número complejo por un escalar, producto de números complejos, división de números complejos, complejo conjugado de un número complejo.
Cuando estudiamos cálculo pensamos que los números reales satisfacen y satisfacerán todas nuestras necesidades aritméticas. Un día aparecen en nuestra vida los números complejos y nos damos cuenta de lo limitado que eran nuestras posibilidades cuando sólo conocíamos a los números reales. Un ejemplo sencillo es querer resolver la siguiente ecuación:
Cuando tratamos de resolverlas nos quedábamos en la respuesta :”no tiene solución” ya que no podemos calcular la raíz cuadrada de -1; y no es una respuesta incorrecta pero si incompleta. La respuesta completamente correcta sería decir : “ no tiene solución dentro del cuerpo de los números reales pero sí dentro del cuerpo de los números complejos”.
¿ Qué son los números complejos ?
Aunque en el párrafo anterior se intuye una de las muchísimas utilidades de los números complejos conviene definir brevemente su forma y sentido. Un número complejo se puede expresar en forma binómica y polar, en estas vídeoclases nos centraremos en su forma binómica.
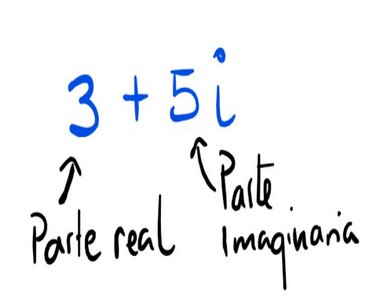
Un número complejo z se escribe de la siguiente forma:
donde a y b son números reales e es la unidad imaginaria. La unidad imaginaria se define como
. De esta forma se llama parte real del número complejo a
y parte imaginaria a
. Todo ésto está explicado perfectamente en las vídeoclases donde explicamos las diferencias entre números complejos, números complejos puros o imaginarios y números reales.
Operaciones con números complejos
En las vídeoclases que se muestran a continuación explico las siguientes operaciones con números complejos en forma binómica:
- Potencias de la unidad imaginaria . Es muy importante, antes de comenzar con las operaciones de números complejos propiamente dichas, saber trabajar con potencias de la unidad imaginaria. El no conocer ésto llevará al alumno a no entender y confundirse en ejercicios básicos de operaciones básicas con complejos.
- Suma y resta de números complejos.
- Producto de números complejos tanto por un escalar como otro número complejo.
- División de números complejos, donde abordamos el concepto de complejo conjugado de un número complejo.
Vídeoclases de Números complejos
A continuación tienes todos los vídeos con las explicaciones anteriormente comentadas. Te animo a que te suscribas al canal de YouTube y a que dejes en los comentarios tus impresiones o cualquier duda que te surja, tanto yo como todos los que vean los vídeos trataremos de ayudarte.

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.
 Suscríbete a mi canal
Suscríbete a mi canal