Contenido
El número PI ha sido un misterio matemático a lo largo de la historia. En esta serie de artículos, exploraremos cómo
ha evolucionado desde sus primeras estimaciones en el Antiguo Egipto hasta su papel crucial en la era digital. Acompáñanos en un viaje a través de los siglos y descubre la trascendental historia de este número irracional, cuya fascinación ha perdurado por generaciones.
Los Primeros Pasos en el Antiguo Egipto
La búsqueda de la relación entre la circunferencia y el diámetro llevó a los antiguos egipcios a dar los primeros pasos en la aproximación de . Aunque sus métodos eran rudimentarios en comparación con los estándares modernos, sus aproximaciones a
ofrecen un vistazo interesante a cómo se abordaban las matemáticas en una de las civilizaciones más antiguas del mundo.
Los egipcios antiguos utilizaban una aproximación simple para alrededor del 1900 a.C. En un papiro matemático conocido como el Papiro de Ahmes, se encontraron fórmulas que indicaban que los egipcios aproximaban
como un valor cercano a 3.125. Si bien esta estimación distaba de ser precisa, permitía a los arquitectos y constructores egipcios trabajar con círculos y formas circulares en sus monumentos y edificios. Aunque estas aproximaciones siguen siendo modestas en comparación con los estándares matemáticos modernos, demuestran el interés y la dedicación de los egipcios para comprender la relación entre la circunferencia y el diámetro de los círculos.

Un ejemplo notable de esta aproximación a se encuentra en la Gran Pirámide de Guiza, construida alrededor del 2560 a.C. Los egipcios, al diseñar la Gran Pirámide, utilizaban una relación en la que el perímetro de la base de la pirámide se relacionaba con su altura y el valor aproximado de
. Aunque su estimación del número PI no era precisa, les permitió construir una de las estructuras más icónicas de la historia de la arquitectura.
En resumen, los primeros pasos en la aproximación de en el Antiguo Egipto revelan el ingenio y la necesidad de los egipcios de trabajar con formas circulares en su arquitectura y construcción. Aunque sus métodos eran simples en comparación con los desarrollos posteriores, sentaron las bases para futuros avances matemáticos y científicos en la búsqueda del valor preciso de
.
Arquímedes y el Método de Agotamiento
Uno de los hitos más significativos en la historia del número Pi se encuentra en el trabajo del matemático griego Arquímedes, quien vivió en el siglo III a.C. Su contribución a la aproximación de es un testimonio del genio matemático que caracterizó a la antigua Grecia.
Arquímedes desarrolló el famoso método de agotamiento, una técnica matemática innovadora que le permitió calcular el número PI con una precisión notable. El método de agotamiento se basaba en la idea de inscribir y circunscribir polígonos regulares en un círculo y, a través de una serie de cálculos, acercarse cada vez más al valor del número PI.
Un ejemplo de su método de agotamiento implica la inscripción y circunscripción de polígonos regulares en un círculo. Arquímedes comenzó con un hexágono regular inscrito en un círculo y otro circunscrito en el mismo círculo. Luego, aumentó el número de lados del polígono, utilizando polígonos de 12, 24, 48 lados, y así sucesivamente.
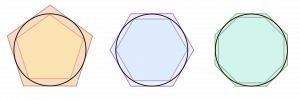
A medida que el número de lados del polígono aumentaba, la estimación de se volvía más precisa. A través de su método de agotamiento, Arquímedes pudo demostrar que
estaba atrapado entre dos valores,
y
. Estas aproximaciones eran asombrosamente precisas para la época y representaron un logro matemático sobresaliente.
El método de agotamiento de Arquímedes no solo se aplicó a la medición de , sino que también tuvo implicaciones en la aproximación de áreas y volúmenes de figuras geométricas. Su enfoque de dividir figuras en componentes más simples y calcularlos por separado allanó el camino para futuros desarrollos en cálculo y análisis matemático.
El trabajo de Arquímedes en la aproximación de y su método de agotamiento influyeron en generaciones posteriores de matemáticos y científicos. Su capacidad para desarrollar técnicas matemáticas innovadoras y lograr estimaciones sorprendentemente precisas de
se destaca como uno de los logros más notables en la historia de las matemáticas.
Arquímedes y su método de agotamiento representan un capítulo esencial en la historia de . Su enfoque ingenioso y sus cálculos precisos sentaron las bases para futuros avances en matemáticas y ciencia, y su legado perdura como un testimonio de la capacidad humana para comprender y dominar conceptos matemáticos profundos.
El número PI y su Papel en la Geometría Antigua
El número PI no se limitó únicamente a ser una constante matemática para la medición de círculos en la antigüedad; también desempeñó un papel esencial en la geometría antigua. Los matemáticos de la antigüedad, como Euclides y Apolonio, exploraron la relación entre y las áreas, los volúmenes y las propiedades geométricas de figuras diversas, lo que influyó significativamente en el desarrollo de la geometría.
Euclides y el número PI
Euclides, el célebre matemático griego que vivió en el siglo III a.C., es famoso por su obra “Elementos”. En esta obra, Euclides abordó la relación de con la circunferencia y su diámetro, estableciendo las bases de la geometría euclidiana. Euclides demostró que el área de un círculo es proporcional al cuadrado de su radio, lo que implicaba una relación intrínseca con el número PI. Aunque Euclides no calculó el valor numérico de
, su trabajo sentó las bases para futuros avances en la comprensión de las figuras circulares.

Apolonio, el número PI y las Cónicas
Apolonio de Pérgamo, un matemático griego que vivió en el siglo III a.C., hizo contribuciones significativas al estudio de las cónicas. Las cónicas son curvas que incluyen círculos, elipses, parábolas e hipérbolas, y Apolonio exploró sus propiedades matemáticas en profundidad. En sus investigaciones, Apolonio utilizó para describir la relación entre las dimensiones de estas curvas y los puntos focales que las definen. Su trabajo en las cónicas contribuyó al desarrollo de la geometría analítica y la representación de figuras geométricas con ecuaciones algebraicas.
Euclides y Apolonio, utilizaron para establecer relaciones fundamentales y sentar las bases para futuros desarrollos en la geometría y la matemática. Sus contribuciones influyeron en la geometría que conocemos hoy y en la comprensión de las figuras geométricas en el mundo antiguo.

El número PI en la Era Islámica
La historia del número PI se extendió al mundo islámico durante la Edad de Oro del Islam, que abarcó desde el siglo VIII hasta el siglo XIII. Durante este período, los estudiosos islámicos realizaron contribuciones significativas al campo de las matemáticas y la geometría, lo que incluyó la aproximación y el estudio de .
Al-Khwarizmi y el número PI
Uno de los matemáticos más influyentes de esta era fue Al-Khwarizmi, cuyo nombre se asocia con la palabra “algoritmo”. Al-Khwarizmi desarrolló métodos para calcular la longitud de un arco de una circunferencia, lo que implicaba el uso del número PI. Su trabajo contribuyó al cálculo de de manera más precisa y al estudio de las matemáticas en el mundo islámico. Propuso un método que involucraba la división de un círculo en 60 sectores y el cálculo de la longitud de un arco en función del ángulo central. Esto permitía una mejor aproximación del número PI y demostraba su conocimiento avanzado en el campo de la trigonometría.

Omar Khayyam y las Cónicas
Omar Khayyam, conocido tanto por sus contribuciones a la poesía como a las matemáticas, también desempeñó un papel en la aproximación de en la geometría. Su trabajo en el estudio de las cónicas, especialmente las parábolas, lo llevó a investigar las propiedades de estas curvas y, en consecuencia, a relacionar
con los aspectos geométricos de las mismas.

Un ejemplo concreto de la influencia del número PI en las matemáticas islámicas se encuentra en el libro “Al-Kitab al-Mansuri” de Al-Biruni, un erudito islámico que vivió en el siglo XI. En este libro, Al-Biruni calculó con una precisión asombrosa y demostró un conocimiento avanzado de las matemáticas y la geometría en su época.

Además de sus contribuciones a la aproximación de , los matemáticos islámicos también influyeron en la transmisión del conocimiento matemático a través de las traducciones y comentarios de obras griegas y romanas. Esto permitió que el conocimiento matemático clásico, incluidas las discusiones sobre
, se preservara y se transmitiera a Europa y otras partes del mundo.
La Era Islámica fue testigo de un florecimiento en el estudio del número PI y su aplicación en la geometría y las matemáticas. Matemáticos islámicos como Al-Khwarizmi, Omar Khayyam y Al-Biruni realizaron investigaciones avanzadas que influyeron en la aproximación de y en la comprensión de las propiedades geométricas de las figuras circulares y cónicas. Sus contribuciones desempeñaron un papel crucial en el desarrollo y la transmisión del conocimiento matemático en la historia.
La Revolución Científica y la Emergencia de Series Infinitas para el número PI
La Revolución Científica en Europa, que tuvo lugar desde el siglo XVII hasta el siglo XVIII, revolucionó la aproximación de y cambió la forma en que los matemáticos se enfrentaban a este número irracional. Matemáticos como John Wallis, James Gregory y otros, marcaron un hito en la historia del número PI al introducir la idea de series infinitas en sus cálculos.
John Wallis y las Fracciones Continuas
John Wallis, un matemático inglés del siglo XVII, realizó contribuciones fundamentales a la aproximación de . Introdujo la notación
para representar el número y desarrolló una serie infinita basada en fracciones continuas que permitía calcular
con una precisión sin precedentes.

La serie infinita de Wallis se conoce como la “fórmula de Wallis” y se representa de la siguiente manera:
Esta serie infinita permitía calcular de manera más precisa a medida que se incluían más términos en la multiplicación. Wallis también estudió las fracciones continuas y demostró que
se podía expresar como una fracción continua infinita, lo que abrió nuevas perspectivas en su aproximación.
James Gregory y las Series de Arcotangentes
El matemático escocés James Gregory también hizo importantes contribuciones a la aproximación del número PI durante la Revolución Científica. Gregory desarrolló una serie infinita que representaba la arcotangente y, mediante esta serie, pudo calcular .

La serie de Gregory para la arcotangente se expresaba de la siguiente manera:
Esta serie permitía calcular la arcotangente de un valor , y Gregory utilizó esta serie para calcular
tomando
. A medida que se incluían más términos en la serie, la aproximación de
se volvía más precisa.
La introducción de series infinitas en la aproximación de marcó un cambio significativo en la forma en que los matemáticos abordaban este número. Estas series permitieron un grado de precisión que anteriormente no se había alcanzado y allanaron el camino para futuros desarrollos en análisis matemático y cálculo.
Un ejemplo concreto de la influencia de las series infinitas en la aproximación de se encuentra en la estimación del número PI de Ludolph van Ceulen, un matemático alemán del siglo XVI, quien calculó
con una precisión de 35 decimales utilizando una serie infinita basada en la fórmula de Wallis. Este logro marcó un hito en la historia del cálculo de
y demostró el poder de las series infinitas en matemáticas.

La Revolución Científica y la introducción de series infinitas por matemáticos como John Wallis y James Gregory marcaron un punto de inflexión en la aproximación del número PI. Estas series permitieron cálculos mucho más precisos y contribuyeron al desarrollo del análisis matemático. Su influencia perdura en la matemática moderna y ha sido fundamental en el cálculo de con un alto grado de precisión.
En la próxima entrega de este artículo trataré El número Pi en las máquinas mecánicas, en la era de la computación, en la cultura popular y sobre todo: Los enigmas no resueltos del número PI.

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.