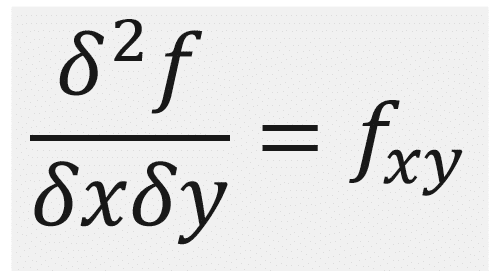La integración por partes es una técnica crucial en el cálculo integral que permite resolver integrales de productos de funciones. En este artículo, te ofreceremos una guía completa sobre cómo aplicar el método de integración por partes, junto con un ejemplo paso a paso para ayudarte a comprender y dominar esta técnica. Si buscas información detallada sobre la integración por partes y cómo aplicarla eficazmente, has llegado al lugar adecuado.
¿Qué es la Integración por Partes y por qué es Importante?
La integración por partes es una herramienta esencial en el campo del cálculo integral. Se basa en una versión modificada de la regla del producto en la derivación y es especialmente útil cuando necesitas encontrar la integral de un producto de dos funciones. Esta técnica es relevante en una amplia gama de aplicaciones matemáticas, científicas e ingenieriles, y es fundamental para resolver problemas en física, estadística, ingeniería y más.
Paso a Paso: Cómo Aplicar la Integración por Partes
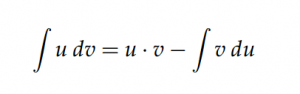
Paso 1: Elección Estratégica de “u” y “dv”
La elección adecuada de las funciones “u” y “dv” es un primer paso crucial. Generalmente, seleccionamos “u” de tal manera que su derivada “du” sea más simple que “u” en sí mismo, y elegimos “dv” de modo que su integral “v” sea más simple que “dv”. Esta elección estratégica se basa en la regla mnemotécnica “LIATE,” que prioriza las siguientes funciones:
- Logaritmos (logaritmos y funciones inversas).
- Inversas trigonométricas.
- Algebraicas (polinomios y funciones algebraicas).
- Trigonométricas.
- Exponenciales.
Paso 2: Cálculo de “du” y “v”
Una vez que hayas elegido “u” y “dv,” calcula la derivada “du” de “u” y la integral “v” de “dv” utilizando las reglas de derivación e integración correspondientes. Esto es esencial para preparar las piezas necesarias para la integración por partes.
Paso 3: Aplicación de la Fórmula de Integración por Partes
La fórmula fundamental de integración por partes es:
Sustituye “u,” “dv,” “du,” y “v” en esta fórmula y realiza los cálculos necesarios para simplificar la integral resultante en el lado derecho de la ecuación.
Paso 4: Resolución de la Integral Resultante
Si es posible, resuelve la integral resultante. En algunos casos, es necesario aplicar el método de integración por partes varias veces o combinarlo con otras técnicas de integración para llegar a una solución final.
Ejemplo de Integración por Partes Paso a Paso
Para que este proceso sea más claro, consideremos un ejemplo práctico:
Siguiendo los pasos mencionados, calculamos esta integral paso a paso:
- u es la
es
por lo tanto:
Sustituyendo:
Es importante tener en cuenta que para poder estudiar con éxito esta materia, debes dominar perfectamente el cálculo de derivadas y las integrales inmediatas.
Conclusión
La integración por partes es una técnica esencial en matemáticas y ciencias, utilizada para resolver problemas que involucran productos de funciones. A través de esta guía completa y el ejemplo paso a paso proporcionado, esperamos haberte ayudado a comprender y aplicar eficazmente este método. Con práctica y dominio de la integración por partes, podrás abordar con confianza una amplia variedad de integrales y resolver problemas más complejos en tus estudios y aplicaciones prácticas. ¡No dudes en explorar más ejemplos y practicar para mejorar tus habilidades en cálculo integral con las clases grabadas que te dejo a continuación!

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.
 Suscríbete a mi canal
Suscríbete a mi canal