El estudio del dominio de una función es un elemento básico en el estudio de funciones. Normalmente, aun siendo una materia que no tiene especial dificultad, los alumnos suelen fracasar al resolver este tipo de ejercicios. En la serie de vídeoclases que os presento se explica de forma detallada y con un lenguaje ameno y comprensible por el alumno los razonamientos en el cálculo del dominio de una función, concretando el procedimiento de cálculo para cada tipo de función.
Todos los conocimientos para poder resolver este tipo de ejercicios se explican en las vídeoclases, siendo mínimos los conocimientos que los alumnos deben tener antes de comenzar estas clases, de esta manera se pretende que nadie abandone debido a la necesidad de tener unas habilidades previas demasiado restrictivas.
Dominio de una función; definición simple
Podemos considerar que una función f no es más que una regla que asigna a cada elemento x del conjunto D otro elemento, sólo uno, del conjunto E y que suele llamarse f(x). (Mirar figura 1).
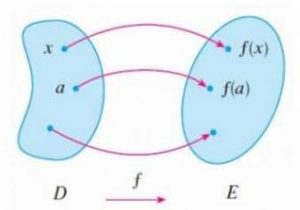
Al conjunto D es lo que llamaremos el dominio de la función f y al conjunto E se le suele llamar como Rango de f o Imagen de f. A la figura anterior se le denomina representación de una función f por medio de un diagrama de flechas; aunque simple es un herramienta muy poderosa para entender qué es el dominio de una función. En la figura 2 se expresa de forma analítica el dominio genérico de la función f de la que estamos tratando.
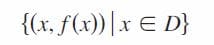
Todos estos detalles quedan perfectamente explicados en las vídeoclases. Siempre recomiendo que se practique lo máximo posible, por lo tanto os animo a que estudiéis todos las vídeoclases de este tema y no os saltéis ninguna.

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.
 Suscríbete a mi canal
Suscríbete a mi canal

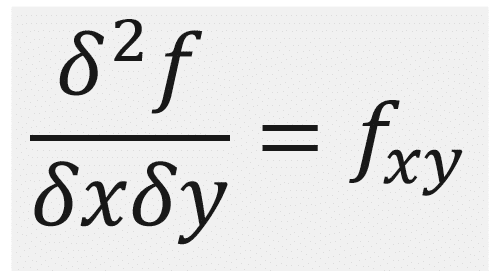
como se resuelven las derivadas parciales
https://www.youtube.com/playlist?list=PLaJK82VXGZpRyFqIhmQksx_FJVn6D1AaR
En esta lista de reproducción lo explico.
Saludos