Calcular las asíntotas de una función suele ser un ejercicio habitual en la asignatura de cálculo. Vamos a encontrar tres tipos de asíntotas:
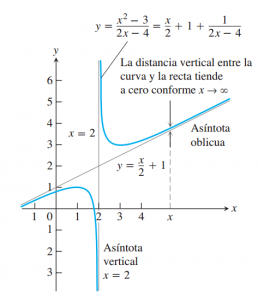
- Asíntotas verticales. Tienen como ecuación la forma x=a, donde a es un número real.
- Asíntotas horizontales. Tienen como ecuación la forma y=b, donde b es un número real.
- Asíntotas oblicuas. Tienen como ecuación la de una recta de la forma y=mx+n, siendo m la pendiente de la recta y n la ordenada en el origen.
En los siguientes vídeos iremos viendo el procedimiento, de forma detallada y paso a paso, para calcular cada una de ellas resolviendo ejercicios típicos que suelen preguntar los profesores en los exámenes.
¿Cómo puedo descargar los apuntes de Asíntotas de una función?
Por cada vídeo de la explicación puedes descargar un archivo en formato PDF donde aparece una versión imprimible de todo lo que explico en el vídeo, de esa manera podrás tener unos apuntes para poder estudiar y repasar lo aprendido en los vídeos. En el siguiente vídeo explico como debes descargar los apuntes de cada vídeo.

Comparte y difunde!
No todo el mundo puede pagar una academia o un profesor particular, por ello, difunde entre tus compañeros de estudio esta web y el canal físicaymates usando para ello vuestras redes sociales y foros de estudiantes. Seguro que tus amigos te lo agradecen.
A continuación tienes el curso, pincha sobre el icono de YouTube, los vídeos aparecen en una lista ordenados por orden de estudio. Comienza por el primero de la lista (el que está más arriba) y llega hasta el último (el que está más abajo). Suscríbete al canal y no olvides regalarme un “me gusta”. Gracias y suerte en tus estudios!
IMPORTANTE : En el reproductor de YouTube debes activar las anotaciones. Pincha en la rueda dentada que aparece en el reproductor abajo a la derecha, en ANOTACIONES debes seleccionar SI.

Espero que todo este material te resulte útil.

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.
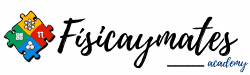


profesor podrías hacer una clase acerca de limites?
Aquí te dejo 11 de mis clases.
Saludos
Desde Argentina te saludo y agradezco, muy claros los conceptos y mejores las explicaciones, muchas gracias.
Gracias por tu comentario.
Saludos