Contenido
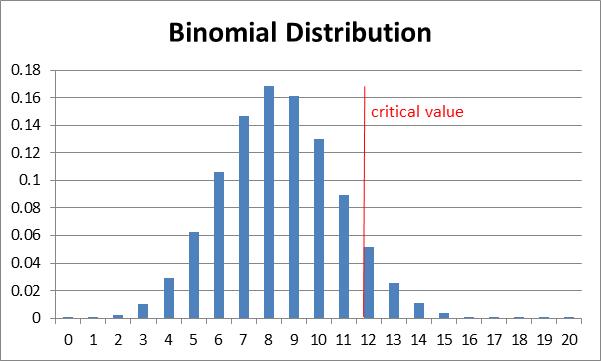
Para comprender mejor la aproximación de Poisson a la distribución de probabilidad binomial hagamos un breve recordatorio de la misma. La distribución de probabilidad binomial, también llamada distribución binómica, es una distribución de probabilidad en la que nuestra variable aleatoria es discreta y nos proporciona el valor de la probabilidad de que en un experimento de Bernoulli que repetimos -veces obtengamos un número
determinado de éxitos. La siguiente expresión nos permite calcular el valor de dicha probabilidad:
(1)
(2)
donde que se lee como:
sobre
, es un número combinatorio también llamado coeficiente binomial.
Tras esta breve introducción a la distribución binomial propongamos el siguiente ejercicio: realizamos un experimento de Bernoulli que repetimos 100 veces (); la probabilidad de éxito es
; la probabilidad de fracaso es
. Hasta aquí son datos del ejercicio. Si nos piden calcular la probabilidad de obtener 4 éxitos tendríamos que sustituir estos valores en la expresión (1), obteniendo:
(3)
donde lo hemos calculado con la expresión (2):
(4)
Un cálculo como este puede resultar bastante engorroso. En estos casos cabe preguntarnos si existe una forma de simplificarlos mediante una buena aproximación. Lo buena que pueda resultar una aproximación nos lo va a decir la diferencia entre el cálculo original y el cálculo por el método de aproximación. Si ambos cálculos son razonablemente similares podemos dar la aproximación como correcta, infiriendo las condiciones en las que la aproximación puede usarse. La solución a la búsqueda de una aproximación a los cálculos anteriores es la Distribución de probabilidad de Poisson.
¿ En qué consiste la aproximación de Poisson de la distribución binomial ?
La aproximación de Poisson a la distribución binomial no es trivial y siempre aplicable; se deben cumplir una serie de condiciones que nos garantizarán que la aproximación es correcta. Las condiciones son las siguientes: que sea grande;
tiene que ser pequeña (es lo que se conoce como un evento raro o poco común); y el producto
.
Si se cumplen las condiciones podremos calcular la expresión (1) mediante la fórmula de la distribución de probabilidad de Poisson:
(5)
donde el valor de . Sustitumos los valores por los datos que nos proporciona el problema que estamos usando en la explicación:
(6)
(7)
Podemos observar que obtenemos el mismo valor que usando la expresión de la distribución binomial (1), pero realizando bastantes menos cálculos y mucho menos engorrosos.
Llegados a este punto parece que hemos encontrado, bajo ciertas condiciones, una buena aproximación a la distribución binomial. Cabe preguntarse cómo es de buena esta aproximación, ya que para hemos obtenido el mismo resultado pero, ¿obtendremos los mismos resultados para
?
¿Cómo de buena es la aproximación de la distribución de Poisson a la distribución binomial?
Abordaremos la respuesta de la pregunta de la forma más sencilla y eficaz posible: vamos a calcular las probabilidades para los casos donde habrá 0,1 y 2 casos de éxito; lo haremos por la distribución binomial y por su aproximación de Poisson y compararemos los cálculos. Nos encontramos con los siguientes resultados:

Podemos observar que la diferencia entre ambos cálculos sólo es apreciable a partir de la tercera cifra decimal. Dicha diferencia supera ligeramente un 2% en el caso más discrepante. Podemos concluir que la aproximación es bastante buena. En general, la aproximación será más correcta cuanto menor sea la probabilidad de éxito y el producto de
.
Invito al lector a continuar la tabla anterior para hasta 7 casos de éxitos y poder comprobar aún mejor que la aproximación es correcta. Si lo has hecho deja tus cálculos en los comentarios de este artículo.
Ejercicio práctico de la aproximación de Poisson en la distribución binomial

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.