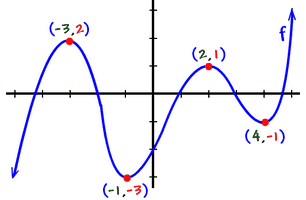
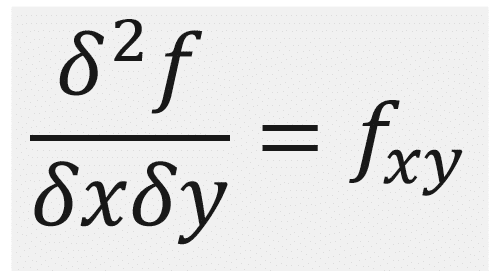Extremos relativos y absolutos de una función

Los extremos relativos y absolutos de una función causan muchos dolores de cabeza entre los estudiantes ya que los confunden. En los siguientes vídeos os voy a explicar de una forma clara la forma de calcularlos y diferenciarlos, tanto analíticamente como gráficamente.

Los extremos relativos se obtienen derivando la función a estudiar e igualando la primera derivada a cero, despejamos la variable,normalmente se llama x, y en caso de que exista solución, esos valores de la x constituyen la coordenada x del punto de los extremos relativos. Lo que no sabemos aún es si son máximos o mínimos, pero son extremos relativos sin ninguna duda. Para poder discernir que tipo de extremos son usaremos el criterio de la segunda derivada.

Los extremos absolutos se calculan usando el “desconocido” Teorema de los valores extremos. Este teorema dice : `Toda función contínua en un intervalo cerrado tiene extremos absolutos (mínimo absoluto y máximo absoluto).´ Es decir, el teorema garantiza la existencia de extremos absolutos para una función continua en un intervalo cerrado pero no dice cómo determinarlos, en los vídeos lo veremos de forma fácil y sencilla.

Extremos Relativos de una Función

Característica	Máximo Relativo	Mínimo Relativo
Definición	Un punto $x = c$ donde $f(c) \geq f(x)$ en un intervalo alrededor de $c$ .	Un punto $x = c$ donde $f(c) \leq f(x)$ en un intervalo alrededor de $c$ .
Condición de la primera derivada	$f'(c) = 0$ o $f'(c)$ no existe.	$f'(c) = 0$ o $f'(c)$ no existe.
Cambio de signo de $f'(x)$	$f'(x)$ cambia de positivo a negativo al pasar por $c$ .	$f'(x)$ cambia de negativo a positivo al pasar por $c$ .
Condición de la segunda derivada	$f''(c) < 0$	$f''(c) > 0$
Visualización	Pico en la gráfica de $f(x)$ .	Valle en la gráfica de $f(x)$ .
Ejemplo	Para $f(x) = x^3 - 3x^2 + 2$ , el punto $x = 0$ es un máximo relativo.	Para $f(x) = x^3 - 3x^2 + 2$ , el punto $x = 2$ es un mínimo relativo.

Extremos relativos y absolutos de una función | Ejercicio resuelto #1

Extremos relativos y absolutos de una función | Ejercicio resuelto #2

Extremos relativos de una función | Ejercicio resuelto #3

Extremos relativos de una función | Ejercicio resuelto #4

Extremos relativos de una función | Ejercicio resuelto #5

Criterio segunda derivada para extremos relativos | Ejercicio resuelto #6

Intervalos de crecimiento de una función | Ejercicio resuelto #6

Francisco Márquez

Estudié Física en la Universidad y como no tuve bastante después volví a estudiar otra carrera, esta vez Ingeniería Informática. Actualmente trabajo como ingeniero de software y el canal de Youtube físicaymates es mi única reminiscencia de mi época como docente.

Vistas: 43.670

Extremos Relativos de una Función

Entradas relacionadas

Deja un comentarioCancelar respuesta